stl multiset example c++

Set and multiset containers sort their elements automatically according to a certain sorting criterion. The difference between the two is that multisets allow duplicates, whereas sets do not.

Figure: Sets and Multisets

To use a set or multiset, you must include the header file <set>:

#include <set>

There, the type is defined as a template class inside namespace std:

namespace std { template <class T, class Compare = less<T>, class Allocator = allocator<T> > class set; template <class T, class Compare = less<T>, class Allocator = allocator<T> > class multiset; }

The elements of a set or multiset may have any type T that is assignable, copyable, and comparable according to the sorting criterion. The optional second template argument defines the sorting criterion. If a special sorting criterion is not passed, the default criterion less is used. The function object less sorts the elements by comparing them with operator <. The optional third template parameter defines the memory model. The default memory model is the model allocator, which is provided by the C++ standard library.

The sorting criterion must define "strict weak ordering." Strict weak ordering is defined by the following three properties:

1. It has to be antisymmetric.
   This means for operator <: If x < y is true, then y < x is false.
   This means for a predicate op(): If op(x,y) is true, then op(y,x) is false.
2. It has to be transitive.
   This means for operator <: If x < y is true and y < z is true, then x < z is true.
   This means for a predicate op(): If op(x,y) is true and op (y,z) is true, then op(x,z) is true.
3. It has to be irreflexive.
   This means for operator <:x < x is always false.
   This means for a predicate op(): op(x,x) is always false.

Based on these properties the sorting criterion is also used to check equality. That is, two elements are equal if neither is less than the other (or if both op(x,y) and op(y,x) are false).

Abilities of Sets and Multisets

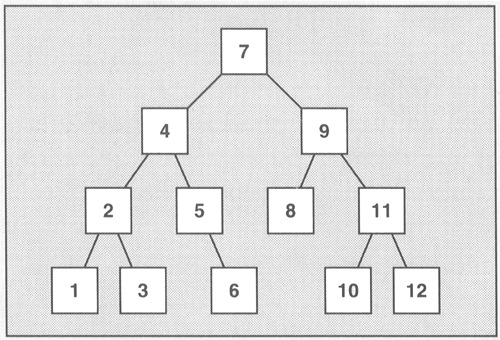
Like all standardized associative container classes, sets and multisets are usually implemented as balanced binary trees. The standard does not specify this, but it follows from the complexity of set and multiset operations.

Figure: Internal Structure of Sets and Multisets

The major advantage of automatic sorting is that a binary tree performs well when elements with a certain value are searched. In fact, search functions have logarithmic complexity. For example, to search for an element in a set or multiset of 1,000 elements, a tree search (which is performed by the member function) needs, on average, one fiftieth of the comparisons of a linear search (which is performed by the algorithm). 

However, automatic sorting also imposes an important constraint on sets and multisets: You may not change the value of an element directly because this might compromise the correct order. Therefore, to modify the value of an element, you must remove the element that has the old value and insert a new element that has the new value. The interface reflects this behavior:

• Sets and multisets don't provide operations for direct element access.
• Indirect access via iterators has the constraint that, from the iterator's point of view, the element value is constant.

Set and Multiset Operations

Create, Copy, and Destroy Operations

Table: lists the constructors and destructors of sets and multisets.

Operation	Effect
set c	Creates an empty set/multiset without any elements
set c(op)	Creates an empty set/multiset that uses op as the sorting criterion
set c1(c2)	Creates a copy of another set/multiset of the same type (all elements are copied)
set c(beg,end)	Creates a set/multiset initialized by the elements of the range [beg,end)
set c(beg,end, op)	Creates a set/multiset with the sorting criterion op initialized by the elements of the range [beg,end)
c.~set()	Destroys all elements and frees the memory

Here, set may be one of the following:

Table: Constructors and Destructors of Sets and Multisets

set	Effect
set<Elem>	A set that sorts with less<> (operator <)
set<Elem,0p>	A set that sorts with 0p
multiset<Elem>	A multiset that sorts with less<> (operator <)
multiset<Elem,0p>	A multiset that sorts with 0p

You can define the sorting criterion in two ways:

1. As a template parameter.
   For example:
   
   std::set<int,std::greater<int> > coll;
   In this case, the sorting criterion is part of the type. Thus, the type system ensures that only containers with the same sorting criterion can be combined. This is the usual way to specify the sorting criterion. To be more precise, the second parameter is the type of the sorting criterion. The concrete sorting criterion is the function object that gets created with the container. To do this, the constructor of the container calls the default constructor of the type of the sorting criterion. See page 294 for an example that uses a user-defined sorting criterion.
   
2. As a constructor parameter.
   In this case, you might have a type for several sorting criteria, and the initial value or state of the sorting criteria might differ. This is useful when processing the sorting criterion at runtime and when sorting criteria are needed that are different but of the same data type. See page 191 for a complete example.

If no special sorting criterion is passed, the default sorting criterion, function object less<>, is used, which sorts the elements by using operator <.

set<int,less<int> > coll;
Note that the sorting criterion is also used to check for equality of the elements. Thus, when the default sorting criterion is used, the check for equality of two elements looks like this:
<
if (! (elem1<elem2 || elem2<elem1))

This has three advantages:

1. You need to pass only one argument as the sorting criterion.
2. You don't have to provide operator == for the element type.
3. You can have contrary definitions for equality (it doesn't matter if operator == behaves differently than in the expression). However, this might be a source of confusion.

However, checking for equality in this way takes a bit more time. This is because two comparisons might be necessary to evaluate the previous expression. Note that if the result of the first comparison yields true, the second comparison is not evaluated.

By now the type name of the container might be a bit complicated and boring, so it is probably a good idea to use a type definition. This definition could be used as a shortcut wherever the container type is needed (this also applies to iterator definitions):

typedef std::set<int,std::greater<int> > IntSet; ... IntSet coll; IntSet::iterator pos;

The constructor for the beginning and the end of a range could be used to initialize the container with elements from containers that have other types, from arrays, or from the standard input. 

Nonmodifying Operations

Sets and multisets provide the usual nonmodifying operations to query the size and to make comparisons (Table below).

Table: Nonmodifying Operations of Sets and Multisets

Operation	Effect
c.size()	Returns the actual number of elements
c.empty ()	Returns whether the container is empty (equivalent to size()==0, but might be faster)
c.max_size()	Returns the maximum number of elements possible
c1 == c2	Returns whether c1 is equal to c2
c1 != c2	Returns whether c1 is not equal to c2 (equivalent to ! (c1==c2) )
c1 < c2	Returns whether c1 is less than c2
c1 > c2	Returns whether c1 is greater than c2 (equivalent to c2<c1)
c1 <= c2	Returns whether c1 is less than or equal to c2 (equivalent to ! (c2<c1) )
c1 >= c2	Returns whether c1 is greater than or equal to c2 (equivalent to !(c1<c2))

Comparisons are provided only for containers of the same type. Thus, the elements and the sorting criterion must have the same types; otherwise, a type error occurs at compile time. For example:

std::set<float> c1; // sorting criterion: std::less<> std::set<float,std::greater<float> > c2; ... if (c1 == c2) { // ERROR: different types ... }

The check whether a container is less than another container is done by a lexicographical comparison. To compare containers of different types (different sorting criteria).

Special Search Operations

Sets and multisets are optimized for fast searching of elements, so they provide special search functions. These functions are special versions of general algorithms that have the same name. You should always prefer the optimized versions for sets and multisets to achieve logarithmic complexity instead of the linear complexity of the general algorithms. For example, a search of a collection of 1,000 elements requires on average only 10 comparisons instead of 500.

Table:- Special Search Operations of Sets and Multisets

Operation	Effect
count (elem)	Returns the number of elements with value elem
find(elem)	Returns the position of the first element with value elem or end()
lower _bound( elem)	Returns the first position, where elem would get inserted (the first element >= elem)
upper _bound (elem)	Returns the last position, where elem would get inserted (the first element > elem)
equal_range (elem)	Returns the first and last position, where elem would get inserted (the range of elements == elem)

The find() member function searches the first element that has the value that was passed as the argument and returns its iterator position. If no such element is found, find() returns end() of the container.

lower_bound() and upper_bound() return the first and last position respectively, at which an element with the passed value would be inserted. In other words, lower_bound() returns the position of the first element that has the same or a greater value than the argument, whereas upper_bound() returns the position of the first element with a greater value. equal_range() returns both return values of lower_bound() and upper_bound() as a pair. Thus, it returns the range of elements that have the same value as the argument. If lower_bound() or the first value of equal_range() is equal to upper_bound() or the second value of equal_range(), then no elements with the same value exist in the set or multiset. Naturally, in a set the range of elements that have the same values could contain at most one element.

The following example shows how to use lower_bound(), upper_bound(), and equal_range():

#include <iostream> #include <set> using namespace std; int main () { set<int> c; c.insert(1); c.insert(2); c.insert(4); c.insert(5); c.insert(6); cout << "lower_bound(3): " << *c.lower_bound(3) << endl; cout << "upper_bound(3): " << *c.upper_bound(3) << endl; cout << "equal_range(3): " << *c.equal_range(3).first << " " << *c.equal_range(3).second << endl; cout << endl; cout << "lower_bound(5): " << *c.lower_bound(5) << endl; cout << "upper_bound(5): " << *c.upper_bound(5) << endl; cout << "equal_range(5): " << *c.equal_range(5).first << " " << *c.equal_range(5).second << endl; }

The output of the program is as follows:

lower_bound(3): 4 upper_bound(3): 4 equal_range(3): 4 4 lower_bound(5): 5 upper_bound(5): 6 equal_range(5): 5 6

If you use a multiset instead of a set, the program has the same output.

Assignments

Sets and multisets provide only the fundamental assignment operations that all containers provide (table below)

For these operations both containers must have the same type. In particular, the type of the comparison criteria must be the same, although the comparison criteria themselves may be different. See page 191 for an example of different sorting criteria that have the same type. If the criteria are different, they will also get assigned or swapped.

Table:- Assignment Operations of Sets and Multisets

Operation	Effect
c1 = c2	Assigns all elements of c2 to c1
c1.swap(c2)	Swaps the data of c1 and c2
swap(c1,c2)	Same (as global function)

Iterator Functions

Sets and multisets do not provide direct element access, so you have to use iterators. Sets and multisets provide the usual member functions for iterators (table below)

Table:- Iterator Operations of Sets and Multisets

Operation	Effect
c.begin()	Returns a bidirectional iterator for the first element (elements are considered const)
c.end()	Returns a bidirectional iterator for the position after the last element (elements are considered const)
c.rbegin()	Returns a reverse iterator for the first element of a reverse iteration
c.rend()	Returns a reverse iterator for the position after the last element of a reverse iteration

As with all associative container classes, the iterators are bidirectional iterators. Thus, you can't use them in algorithms that are provided only for random access iterators (such as algorithms for sorting or random shuffling).

More important is the constraint that, from an iterator's point of view, all elements are considered constant. This is necessary to ensure that you can't compromise the order of the elements by changing their values. However, as a result you can't call any modifying algorithm on the elements of a set or multiset. For example, you can't call the remove() algorithm to remove elements because it "removes" by overwriting "removed" elements the with following arguments (see Section 5.6.2, for a detailed discussion of this problem). To remove elements in sets and multisets, you can use only member functions provided by the container.

Inserting and Removing Elements

Table below shows the operations provided for sets and multisets to insert and remove elements.As usual by using the STL, you must ensure that the arguments are valid. Iterators must refer to valid positions, the beginning of a range must have a position that is not behind the end, and you must not try to remove an element from an empty container.

Inserting and removing happens faster if, when working with multiple elements, you use a single call for all elements rather than multiple calls.

Table:- Insert and Remove Operations of Sets and Multisets

Operation	Effect
c. insert(elem)	Inserts a copy of elem and returns the position of the new element and, for sets, whether it succeeded
c. insert(pos, elem)	Inserts a copy of elem and returns the position of the new element (pos is used as a hint pointing to where the insert should start the search)
c. insert (beg,end)	Inserts a copy of all elements of the range [beg,end) (returns nothing)
c. erase(elem)	Removes all elements with value elem and returns the number of removed elements
c. erase(pos)	Removes the element at iterator position pos (returns nothing)
c. erase(beg,end)	Removes all elements of the range [beg,end) (returns nothing)
c. clear()	Removes all elements (makes the container empty)

Note that the return types of the insert functions differ as follows:

• Sets provide the following interface:
  
  pair<iterator,bool> insert(const value_type& elem); iterator insert(iterator pos_hint, const value_type& elem);
  
• Multisets provide the following interface:
  
  iterator insert(const value_type& elem); iterator insert(iterator pos_hint, const value_type& elem);
  

The difference in return types results because multisets allows duplicates, whereas sets do not. Thus, the insertion of an element might fail for a set if it already contains an element with the same value. Therefore, the return type of a set returns two values by using a pair structure,

1. The member second of the pair structure returns whether the insertion was successful.
2. The member first of the pair structure returns the position of the newly inserted element or the position of the still existing element.

In all other cases, the functions return the position of the new element (or of the existing element if the set contains an element with the same value already). The following example shows how to use this interface to insert a new element into a set. It tries to insert the element with value 3.3 into the set c:

std::set<double> c; if (c.insert(3.3).second) { std::cout << "3.3 inserted" << std::endl; } else { std::cout << "3.3 already exists" << std::endl; }

If you also want to process the new or old positions, the code gets more complicated:

//define variable for return value of insert() std::pair<std::set<float>::iterator,bool> status; //insert value and assign return value status = c.insert(value); //process return value if (status.second) { std::cout << value << " inserted as element " } else { std::cout << value << " already exists as element " } std::cout << std::distance(c.begin().status.first) + 1 << std::endl;

The output of two calls of this sequence might be as follows:

8.9 inserted as element 4 7.7 already exists as element 3

Note that the return types of the insert functions with an additional position parameter don't differ. These functions return a single iterator for both sets and multisets. However, these functions have the same effect as the functions without the position parameter. They differ only in their performance. You can pass an iterator position, but this position is processed as a hint to optimize performance. In fact, if the element gets inserted right after the position that is passed as the first argument, the time complexity changes from logarithmic to amortized constant. The fact that the return type for the insert functions with the additional position hint doesn't have the same difference as the insert functions without the position hint ensures that you have one insert function that has the same interface for all container types. In fact, this interface is used by general inserters. To remove an element that has a certain value, you simply call erase():

std::set<Elem> coll; ... //remove all elements with passed value coll.erase(value);

Unlike with lists, the erase() member function does not have the name remove(). It behaves differently because it returns the number of removed elements. When called for sets, it returns only 0 or 1. If a multiset contains duplicates, you can't use erase() to remove only the first element of these duplicates. Instead, you can code as follows:

std::multiset<Elem> coll; ... //remove first element with passed value std::multiset<Elem>::iterator pos; pos = coll.find (elem); if (pos != coll.end()) { coll.erase(pos); }

You should use the member function find() instead of the find() algorithm here because it is faster. Note that there is another inconsistency in return types here. That is, the return types of the erase() functions differ between sequence and associative containers as follows:

1. Sequence containers provide the following erase() member functions:
   
   iterator erase(iterator pos); iterator erase(iterator beg, iterator end);
   
2. Associative containers provide the following erase() member functions:
   
   void erase(iterator pos); void erase(iterator beg, iterator end);
   

The reason for this difference is performance. It might cost time to find and return the successor in an associative container because the container is implemented as a binary tree. However, as a result, to write generic code for all containers you must ignore the return value.

Exception Handling

Sets and multisets are node-based containers, so any failure to construct a node simply leaves the container as it was. Furthermore, because destructors in general don't throw, removing a node can't fail. However, for multiple-element insert operations, the need to keep elements sorted makes full recovery from throws impractical. Thus, all single-element insert operations support commit-or-rollback behavior. That is, they either succeed or they have no effect. In addition, it is guaranteed that all multiple-element delete operations always succeed. If copying/assigning the comparison criterion may throw, swap() may throw.

Examples of Using Sets and Multisets

The following program demonstrates some abilities of sets:


#include <iostream> #include <set> using namespace std; int main() { /*type of the collection: *-no duplicates *-elements are integral values *-descending order */ typedef set<int,greater<int> > IntSet; IntSet coll1; // empty set container //insert elements in random order coll1.insert(4); coll1.insert(3); coll1.insert(5); coll1.insert(1); coll1.insert(6); coll1.insert(2); coll1.insert(5); //iterate over all elements and print them IntSet::iterator pos; for (pos = coll1.begin(); pos != coll1.end(); ++pos) { cout << *pos << ' '; } cout << endl; //insert 4 again and process return value pair<IntSet::iterator,bool> status = coll1.insert(4); if (status.second) { cout << "4 inserted as element " << distance (coll1.begin(),status. first) + 1 << endl; } else { cout << "4 already exists" << endl; } //assign elements to another set with ascending order set<int> coll2(coll1.begin(), coll1.end()); //print all elements of the copy copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; //remove all elements up to element with value 3 coll2.erase (coll2.begin(), coll2.find(3)); //remove all elements with value 5 int num; num = coll2.erase (5); cout << num << " element(s) removed" << endl; //print all elements copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; }

At first, the type definition

typedef set<int,greater<int> > IntSet;

defines a short type name for a set of ints with descending order. After an empty set is created, several elements are inserted by using insert ():

IntSet coll1; coll1.insert(4); ...

Note that the element with value 5 is inserted twice. However, the second insertion is ignored because sets do not allow duplicates. After printing all elements, the program tries again to insert the element 4. This time it processes the return values of insert().

The statement

set<int> coll2(coll1.begin(), coll1. end());

creates a new set of ints with ascending order and initializes it with the elements of the old set.

set<int,less<int> > coll2; copy (coll1.begin(), coll1. end(), inserter(coll2,coll2.begin()));

Both containers have different sorting criteria, so their types differ and you can't assign or compare them directly. However, you can use algorithms, which in general are able to handle different container types as long as the element types are equal or convertible.

The statement

coll2.erase (coll2.begin(), coll2.find(3));

removes all elements up to the element with value 3. Note that the element with value 3 is the end of the range, so that it is not removed. Lastly, all elements with value 5 are removed:

int num; num = coll2.erase (5); cout << num << " element(s) removed" << endl;

The output of the whole program is as follows:

6 5 4 3 2 1 4 already exists 1 2 3 4 5 6 1 element(s) removed 3 4 6

For multisets, the same program looks a bit differently and produces different results:

#include <iostream> #include <set> using namespace std; int main() { /*type of the collection: *-duplicates allowed *-elements are integral values *-descending order */ typedef multiset<int,greater<int> > IntSet; IntSet coll1, // empty multiset container //insert elements in random order coll1.insert(4); coll1.insert(3); coll1.insert(5); coll1.insert(l); coll1.insert(6); coll1.insert(2); coll1.insert(5); //iterate over all elements and print them IntSet::iterator pos; for (pos = coll1.begin(); pos != coll1.end(); ++pos) { cout << *pos << ' '; } cout << endl; //insert 4 again and process return value IntSet::iterator ipos = coll1.insert(4); cout << "4 inserted as element " << distance (coll1.begin(),ipos) + 1 << endl; //assign elements to another multiset with ascending order multiset<int> coll2(coll1.begin(), coll1.end()); //print all elements of the copy copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; //remove all elements up to element with value 3 coll2.erase (coll2.begin(), coll2.find(3)); //remove all elements with value 5 int num; num = coll2.erase (5); cout << num << " element(s) removed" << endl; //print all elements copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; }

In all cases type set was changed to multiset. In addition, the processing of the return value of insert() looks different:

IntSet::iterator ipos = coll1.insert(4); cout << "4 inserted as element " << distance (coll1.begin(),ipos) + 1 << endl;

Because multisets may contain duplicates, the insertion can fail only if an exception gets thrown. Thus, the return type is only the iterator position of the new element.

The output of the program changed as follows:

6 5 5 4 3 2 1 4 inserted as element 5 1 2 3 4 4 5 5 6 2 element(s) removed 3 4 4 6

Example of Specifying the Sorting Criterion at Runtime

Normally you define the sorting criterion as part of the type, either by passing it as a second template argument or by using the default sorting criterion less<>. However, sometimes you must process the sorting criterion at runtime, or you may need different sorting criteria with the same data type. In this case, you need a special type for the sorting criterion — one that lets you pass your sorting details at runtime. The following example program demonstrates how to do this:

#include <iostream> #include <set> #include "print.hpp" using namespace std; //type for sorting criterion template <class T> class RuntimeCmp { public: enum cmp_mode {normal, reverse}; private: cmp_mode mode; public: //constructor for sorting criterion //-default criterion uses value normal RuntimeCmp (cmp_mode m=normal) : mode(m) { } //comparision of elements bool operator() (const T& t1, const T& t2) const { return mode == normal ? t1 < t2 : t2 < t1; } //comparision of sorting criteria bool operator== (const RuntimeCmp& rc) { return mode == rc.mode; } }; //type of a set that uses this sorting criterion typedef set<int,RuntimeCmp<int> > IntSet; //forward declaration void fill (IntSet& set); int main() { //create, fill, and print set with normal element order //-uses default sorting criterion IntSet coll1; fill(coll1); PRINT_ELEMENTS (coll1, "coll1: "); //create sorting criterion with reverse element order RuntimeCmp<int> reverse_order(RuntimeCmp<int>::reverse); //create, fill, and print set with reverse element order IntSet coll2(reverse_order); fill(coll2); PRINT_ELEMENTS (coll2, "coll2: "); //assign elements AND sorting criterion coll1 = coll2; coll1.insert(3); PRINT_ELEMENTS (coll1, "coll1: "); //just to make sure... if (coll1.value_comp() == coll2.value_comp()) { cout << "coll1 and coll2 have same sorting criterion" << endl; } else { cout << "coll1 and coll2 have different sorting criterion" << endl; } } void fill (IntSet& set) { //fill insert elements in random order set.insert(4); set.insert(7); set.insert(5); set.insert(1); set.insert(6); set.insert(2); set.insert(5); }

In this program, RuntimeCmp<> is a simple template that provides the general ability to specify, at runtime, the sorting criterion for any type. Its default constructor sorts in ascending order using the default value normal. It also is possible to pass RuntimeCmp<>::reverse to sort in descending order.

The output of the program is as follows:

coll1: 1 2 4 5 6 7 coll2: 7 6 5 4 2 1 coll1: 7 6 5 4 3 2 1 coll1 and coll2 have same sorting criterion

Note that coll1 and coll2 have the same type, which is used in fill(), for example. Note also that the assignment operator assigns the elements and the sorting criterion (otherwise an assignment would be an easy way to compromise the sorting criterion).

-----------------------------------------------------------------
See Also:
-----------------------------------------------------------------

• Complete Tutorial of C++ Template's
• Standard Template Library Tutorial
• Inter Process Communication Tutorial
• Advance Programming in C & C++

-----------------------------------------------------------------

The Art of Learning with Innovation,
eLearning Courses for C and C++ Programming Language - The Most appreciated course !!!

Copyright © ccplusplus.com